In the card game SET!, players are shown an array of 12 (or more) symbol cards and try to identify a so-called 3-card set among these cards as quickly as possible.

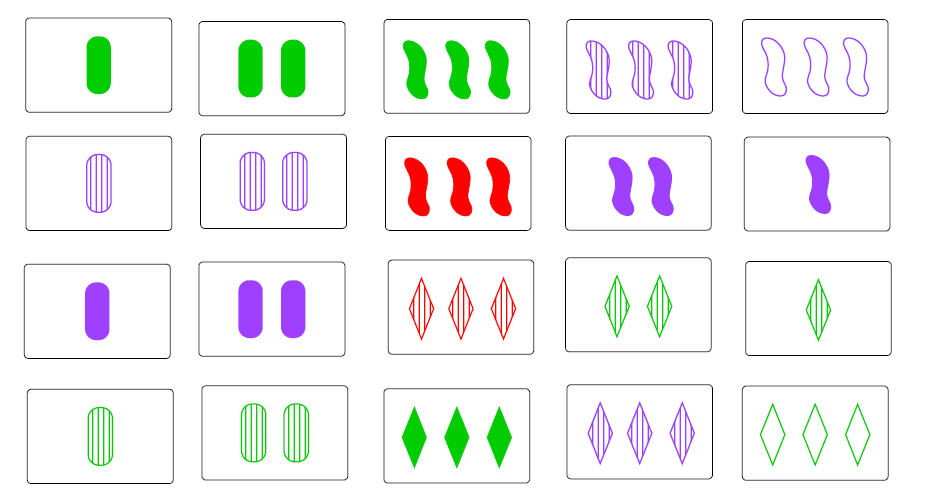
Set (stylized as SET) is a real-time card game designed by Marsha Falco in 1974 and published by Set Enterprises in 1991. The deck consists of 81 unique cards that vary in four features across three possibilities for each kind of feature: number of shapes (one, two, or three), shape (diamond, squiggle, oval), shading (solid, striped, or open), and color (red, green, or purple). PlayMonster proudly makes SET games! The award-winning family and educational games include SET®, Quiddler®, Five Crowns®, Karma®, WordSpiel® and Zangle®, plus brand extensions! These card games focus on fun, perception and challenge for players of all ages and skill levels while offering unlimited replay value. I love to add math games to our curriculum and today I want to show you how to play one of my favorite card games. SET was introduced to me years ago by a go. SET (card game) Play Monster Age 8+ This review was submitted by Kaushiki Sreeja Marupalli, a seventh grader from North Carolina. SET is a really fun card game which is more than just luck. You need to use pattern-finding skills and speed to make sure you find the most sets. Think of it as an intense memory game.

A card has four attributes (number, shape, color and shading), each of which can take 3 possible values. In a set, for each attribute, all three cards should have either the same value, or the three different values.

This recipe solves the problem of finding all sets within an array of an arbitrary number of cards, showing some clever optimizations and celebrating the clarity of Python in expressing the algorithms.

A card is basically represented as a 4-tuple of integers, each of which can be 0, 1 or 2. This is an example of three cards forming a set:

Set Card Game Instructions

And these cards do not form a set:

Indeed, all attributes have to pass the test.

Around the 4-tuple we construct a small class Card; this allows us to use a more object-oriented style (card0.isset(card1,card2) instead of modulename.isset(card0,card1,card2)) and also to use an alternative representation.

The obvious way to find all sets in a table of n cards is to check all 3-card combinations using a three-level nested loop, like Table.findsets_gnt() does. Not every level needs to loop over n cards: this would visit each 3-card combination 6 separate times (and moreover, investigate combinations that include the same card more than once). Instead, the loops are constructed such that for each 3-card combination, the first card (in table order) is represented by the outer loop variable, the second by the middle loop variable, and the third by the inner loop variable.Each combination is checked; when it is a set, it is appended to the list of found sets.

The first step to optimization is to realize that an individual attribute passes the set-test if and only if the sum of the values on the three cards for this attribute, modulo 3, equals 0: (0+0+0)%30, (1+1+1)%30, (2+2+2)%30, and (0+1+2)%30. This is exploited in Card.isset_mod() and Table.findsets_gnt_mod().

The second optimization step is to exploit the fact that each combination of two cards (card0,card1) forms a set with one unique other card. This card can be determined by setting card2.attrs[i] = (-card0.attrs[i]-card1.attrs[i])%3 for all i (as implemented in Card.thirdcard_simple()). There are faster ways for checking whether this card is on the table than by looping over the remaining cards. In Table.findsets_simple(), we put all the table cards in a dictionary have; a dictionary lookup is performed using the card's hash value instead of looping over the dictionary items. In addition, we need to check whether the third card is behind the other two cards in table order, otherwise sets are doubly counted.

In the final optimization, we represent the 4 attributes in one integer, with 2 bits per attribute:

If we can devise a function that calculates (-x-y)%3 in this representation using bitwise operators, we can apply it to all 8 bits at the same time. And indeed we can (with a little help from Karnaugh maps); the result is Card.thirdcard_fast(). With this 8-bit representation of cards, we also chose to put the table cards in a 256-element list; we only need to index the list to check whether a card is on the table, and this is probably faster than a dictionary lookup.

Timing results

Using ipython. Live sports betting lines.

Naturally, the differences become more pronounced with a table of 81 cards.

Set Card Game Online

Of course, the motivation for this recipe aren't the milliseconds but the fun of computer science puzzles!